Jag gillade Matlab från första början, det var lätt att lära sig och syntaxen var ganska enkel.
Största fördelen var matrishanteringen som är fantastiskt enkel jämfört med t.ex C. I Matlab kan
man addera två matriser direkt utan loopar. Man kan hoppa över de flesta variabeldeklarationer,
även om jag brukar göra det, speciellt med vektorer och matriser.
Det jag hittills gjort i Matlab är:
  • Simulering av LQ-reglering samt inhämtning av mätdata och visualisering av denna,
    och grafiskt interface.
  • Bildbehandling
  • Numerisk analys, och grafiskt interface med möjlighet att spara funktioner.
  • RFC-analys, och grafiskt interface med filhantering
  • Ett antal olika spel som t.ex. MasterMind
  • Matematiska experiment i största allmänhet som olika attraktorer
Kanske dags att fixa ett "Hello world" program i Matlab också, så håll till godo:

display('Hello world');

Eftersom jag jobbat en hel del i Matlab fick jag häromdagen för mig att testa
bildbehandling i Matlab. Eftersom jag inte kommit så lågnt ännu finns inga GUI
eller häftiga funktioner, men jag har gjort en negativfunktion och svartvit-
funktion hittills. Dessa är förvånansvärt enkla (i kodlängd). Jag har valt
att göra så här:
[AA,Ftab] = imread('PICT0082.JPG','jpeg');
ImgSize = size(AA);
matris255 = 255*ones(ImgSize);
AAInv = matris255-double(AA);
Att göra om bilden till svartvit gick jag tillväga på följande vis:

AA=double(AA);
A1=round((AA(:,:,1)+AA(:,:,2)+AA(:,:,3))/3);
A2(:,:,1)=A1;
A2(:,:,2)=A1;
A2(:,:,3)=A1;
För att visa bilderna används kommandot image(A);, eftersom detta
vill ha en matris som argument med elementen i spannet 0 och 1 måste värdena i
matrisen omvandlas eftersom dessa ligger mellan 0 och 255. Detta görs enklast
med t.ex. uint8 För att rita upp bilden är det enklast att göra så här:

figure; %För att skapa ett nytt graffönster.
image(uint8(A2));
 Som ni ser går det utmärkt att "bunta" ihop kommandon i Matlab vilket kan bli
förvirrande om det är fler än låt säga tre-fyra stycken.

För att visa hur det blir med dessa enkla funktioner utgår jag från denna bild:

Negativet av denna bild blir så här:

Omgjord till svartvitt blev det så här:


För att göra bilden suddig eller använda ett gaussiskt filter om man så vill
finns det olika varianter. Denna version kan knappast kallas gaussiskt filter,
snarare en klumpig och ganska brutal variant av utsmetning (bättre kommer):

A3 = ones(size(AA,1),size(AA,2),size(AA,3));
A3(1,:,:) = AA(1,:,:);
A3(size(AA,1),:,:) = AA(size(AA,1),:,:);
A3(:,1,:) = AA(:,1,:);
A3(:,size(AA,2),:) = AA(:,size(AA,2),:);

for ii = 2:size(AA,1)-1
for jj = 2:size(AA,2)-1
A3(ii,jj,1) = round(sum(sum(AA(ii-1:ii+1,jj-1:jj+1,1)))/9);
A3(ii,jj,2) = round(sum(sum(AA(ii-1:ii+1,jj-1:jj+1,2)))/9);
A3(ii,jj,3) = round(sum(sum(AA(ii-1:ii+1,jj-1:jj+1,3)))/9);
end
end
Så resultatet (originalet till vänster):

Efter att ha letat runt lite på olika sidor på Internet har jag knåpat ihop
en kodsnutt som gör bilden suddigare med hjälp av en gaussmatris. Jag utgick
ifrån denna funktion: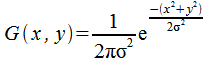



Med radien 3 och σ = 1 fÃ¥s följande matris: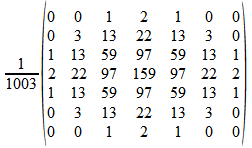



För att räkna ut matrisvärdena använde jag följande for-loop:

for x = 1:radius*2+1
for y = 1:radius*2+1
gauss(x,y) = 1/(2*pi*sigma)*exp(-(abs((radius+1)-x)^2+abs((radius+1)-y)^2)/(2*sigma^2));
end
end
För att använda sig av gaussfiltret har jag utökat bilden med 2*radius pixlar
vilket medför att jag får en ram runt bilden i en viss färg. Detta påverkar
resultatet markant, desto mindre bild desto större påverkan.
När detta är gjort körs filtret, se kod nedan:

A4 = zeros(size(AA,1)+2*radius,size(AA,2)+2*radius,size(AA,3));
AA1 = size(AA,1);
AA2 = size(AA,2);
AA3 = size(A4,1);
AA4 = size(A4,2);

A4(1:radius,1:radius,:,:) = A4(radius+1:2*radius,1:radius,:); %Övre vänsterhörn.
A4(AA3-radius+1:AA3,1:radius,:) = A4(AA3-2*radius+1:AA3-radius,1:radius,:); %Nedre vänsterhörn.
A4(1:radius,AA4-radius+1:AA4,:) = A4(1:radius,AA2+1:AA2+radius,:); %Övre högerhörn.

A4(AA3-radius+1:AA3,AA4-radius+1:AA4,:) = A4(AA3-2*radius+1:AA3-radius,AA4-radius+1:AA4,:); %Nedre högerhörn.
A4(radius+1:AA1+radius,radius+1:AA2+radius,:) = AA; %Mittenbiten, alltså hela bilden.
figure;
image(uint8(A4));axis off;axis equal;
A5 = zeros(size(AA,1)+2*radius,size(AA,2)+2*radius,size(AA,3));

for ii = radius+1:1:AA1+radius
for jj = radius+1:1:AA2+radius
A5(ii,jj,1) = round(sum(sum(double(A4(ii-radius:ii+radius,jj-radius:jj+radius,1)).*gauss)));
A5(ii,jj,2) = round(sum(sum(double(A4(ii-radius:ii+radius,jj-radius:jj+radius,2)).*gauss)));
A5(ii,jj,3) = round(sum(sum(double(A4(ii-radius:ii+radius,jj-radius:jj+radius,3)).*gauss)));
end
end
A1 = A5(radius+1:AA1+radius,radius+1:AA2+radius,:);
figure;
image(uint8(A1));axis off;axis equal;

 Resultatet med ovanstående värden blev så här:






Som jämförelse ser ni här uppifrån och ner: gaussisk "suddfunktion", originalbilden,
och den med oviktad "suddfunktion".

Numerisk analys

För att göra ett tvärt kast som kanske inte är så tvärt när man tänker efter lite.
Under min utbildning kom jag i kontakt med numerisk analys, ett ämne jag "föll för"
direkt. Troligen på grund av en inspirerande lärare. Så jag satte mig ner för ett tag
sedan och försökte sammanfatta, kanske inte hela kursen men de delar som jag fann mest
intressanta.

Nedan ser ni en skärmdump av det GUI jag gjorde för att underlätta användandet:

Klicka för större bild
För att skapa ovanstående GUI har jag använt följande kod:


Den ändring som kan behöva göras i filen ovan för att det skall fungera är följande:
'FileName','C:\MATLABR11\work\Lek\NA\Analys4\Analys4.m',
Det som behöver göras är att ändra sökvägen till den som stämmer för dig.

För att man skall kunna använda filen ovan till något så krävs följande fil:

Rain-Flow Count (RFC)

RFC används för att identifiera och beräkna cykler för komponenter, t.ex. jetmotorer.
Se vidare: http://en.wikipedia.org

Klicka för större bild
Tyvärr använder denna applikation ett flertal filer så om du är intresserad får du gärna
kontakta mig så skickar jag över filerna till dig så att du kan testa. Skicka gärna via detta formulär: MKarlsson.eu

Tärningsspel

Detta spel går ut på att med hjälp av te två slumpmässiga tärningarna släcka ner rutorna 1-9.
Antingen var för sig eller summan av de två.